Infinite Powers: How Calculus Reveals the Secrets of the Universe
引言
写给每个人的微积分读物
由微积分主宰的世界
应用数学家 波动方程 电场 磁场 他不仅利用微积分预测出电磁波的存在，还解开了一个古老的谜题：光的性质是什么？他 意识到，光就是一种电磁波。
微积分不只是一种语言
微积分和其他数学形式一样，不仅是一种语言，还是一个非常强大的推理系统
不合理的有效性
Albert Einstein 写下「世界的永恒之谜在于它的可理解性」
无穷原则
无穷原则 微积分 Calculus 微积分可分为两个步骤：切分和重组 微分 Differential of a function 切分过程总是涉及无限精细的减法运算，用于量化各部分之间的差异，这个部分叫作微 分学 积分 Integral 重组过程则总是涉及无限的加法运算，将各个部分整合成原来的整体，这个部分叫作积 分学。
形状、物体、液体、运动和时间间隔等都是微积分的应用对象，它们全部或者几乎都是 连续的。
微积分忽略了原子和其他不可切分实体造成的不便，这不是因为它们不存在，而是因为 假装它们不存在会大有帮助 更广泛地说，被微积分建模为连续体的实体类型，包含了我们能想到的几乎所有东西
石巨人与无穷
曲线、运动和变化
有三个谜题促进了微积分的发展，它们分别是曲线之谜、运动之谜和变化之谜。 曲线 曲线的含义非常宽泛，指任何形式的曲线、曲面或曲面体，比如橡皮筋、结婚戒指、漂 浮的气泡、花瓶的轮廓或者一根意大利香肠
有些几何学家坚持认为“曲线事实上是由平直部件构成的”，这种观点带来了突破性进展 速度不停变化的运动是由无穷多个无限短暂的匀速运动组成的 受激发射 在某些情况下，穿过物质的光能激发出更多波长相同和传播方向相同的光，并通过一种 连锁反应产生大量的光，形成强烈的相干光束
根据量子力学，在微观尺度上，电子的运动轨迹会发生抖动，变得模糊不清和难以确定， 所以我们需要将电子的行为描述成概率波，它不再遵循牛顿运动定律
1. 无穷的故事
每年夏季，在尼罗河的洪水泛滥过后，土地测量员必须重新划定农田的边界线。后来，人 们基于这项活动给研究形状的领域起了个名字：几何学。
在数学上，圆体现的是没有变化的变化。一个点绕圆周运动，尽管它的方向一直在变，但 它到圆心的距离始终不变
圆还具有对称性
作为桥梁的无穷
比萨证明
它的周长（用字母C表示）是
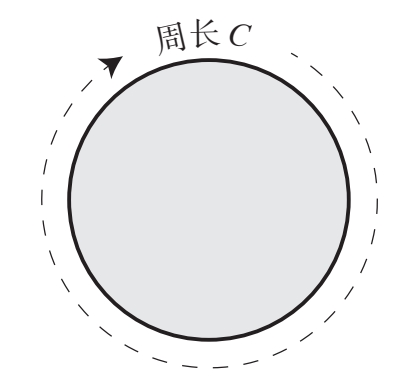
极限与墙之谜
0.333…的故事
无穷多边形的故事
无穷的魅力和危险
极限通常比逼近它们的近似值简单。圆比所有接近它的多边形（有很多突起）都更简单， 也更优美
除数为 0 的禁忌
除数为0会召唤出无穷
实无穷之罪
实无穷 无穷 在切分线段的例子中，潜无穷意味着，尽管这条线段可以被分成任意多段，但数量总是 有限的，每小段的长度也都不为0
芝诺悖论
在芝诺看来，尽管感官告诉我们这不是事实，但它实际上欺骗了我们；改变是一种错觉。 在芝诺悖论中，有三个尤其知名和有影响力。第一个是二分法悖论，它与墙之谜类似， 但更加令人沮丧
第二个是阿喀琉斯与乌龟悖论 律师和逻辑学家把这种修辞策略称为“归谬法
芝诺悖论走向数字化
第三个是飞矢不动悖论，芝诺用它来驳斥另一种可能性，即空间和时间从根本上说是离 散的，这意味着它们由不可分割的微小单元（类似于空间像素和时间像素）组成。这个 悖论的内容是：如果空间和时间是离散的，飞矢就未曾移动，因为在每一个瞬间（一个 时间像素），飞矢都在某个确定的位置（一组特定的空间像素）上。由此可以推断，在 任何给定的瞬间，飞矢都是静止不动的。它也不会在两个瞬间之间移动，因为根据假设， 两个瞬间之间是没有时间的。所以，飞矢从未移动。 在很多实际应用中，只要我们把事物切分得足够细致，离散就可以替代连续。
当芝诺悖论遇上量子力学
量子隧穿效应 量子力学对它做出的解释是，电子可以用概率波来描述
概率波遵循薛定谔方程 薛定谔方程的解表明，一小部分电子概率波会出现在难以逾越的障碍的另一边
从微积分到理论物理学，它们都建立在空间和时间具有连续性的假设基础之上
极限尺度是由自然界的三大基本常量决定的，我们无法左右。 第一个是引力常量G，它衡量的是宇宙中的引力强度 第二个常量ħ反映了量子效应的强度，它出现在海森伯的不确定性原理和薛定谔的量子力 学波动方程中 第三个常量是光速c，它是宇宙的极限速度，任何一种信号的传播速度都无法超过c
普朗克长度[4]。它的公式是： \({\displaystyle \ell _{P}={\sqrt {\frac {\hbar G}{c^{3}}}}\cong 1.616229(38)\times 10^{-35}}公尺\) 普朗克长度约为10–35米
2. 驾驭无穷的勇士
浮力原理（浸在流体中的物体所受的浮力与被该物体排开的流体重量大小相等 杠杆定律（当且仅当杠杆两端重物的重量与它们到支点的距离成反比时，杠杆才会平衡
夹逼法与圆周率
圆周率之道
圆周率具有某些相互矛盾的属性。一方面，它代表秩序，这一点主要体现在圆的形状上， 长久以来圆都被视为完美和永恒的象征。另一方面，圆周率又是无序的，看上去零落散 乱，数字排列也没有明显的规律，或者至少我们尚未发现其中的规律。圆周率难以捉摸， 神秘莫测，而且永远遥不可及。这种有序与无序的混合正是它的魅力所在。
圆周率是微积分的产物，它被定义为无尽过程的难以达到的极限。但是，与一系列坚定 地逼近圆的多边形或者每次朝着墙前进一半距离的倒霉步行者不同，圆周率既没有可见 的终点，也没有可知的极限。然而，圆周率确实存在。它就在那里，它的定义也很清晰， 即我们能看见的两个长度（圆的周长和直径）之比。尽管这个比率定义了圆周率，描述 得也非常清晰，但数本身却从我们的指缝中溜走了。 有着阴阳二元性的圆周率就像整个 微积分的缩影。圆周率是圆与直线之间的一扇门，是一个无限复杂的数，也是秩序与混 沌之间的平衡。
立体主义与微积分
从切面看，抛物线是一条优美的对称曲线，它的正中间有一条对称线，被称为轴（图2–9）。
想象一下，用一把切肉刀截切一顶锥形纸帽或者一个锥形纸杯，根据切肉刀截切锥体的
陡度，它可以切出不同类型的曲线。如果它平行于锥体底面截切，就会得到一个圆（图
2–6）。
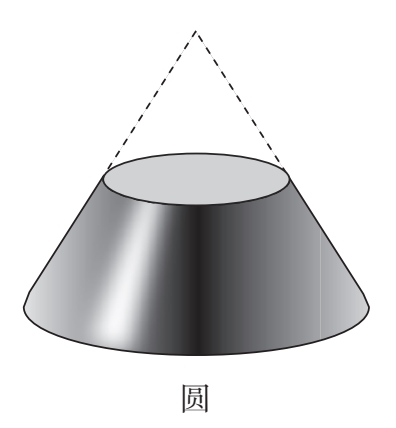如果它截切的角度略微倾斜，就会得到一个椭圆（图2–7）。
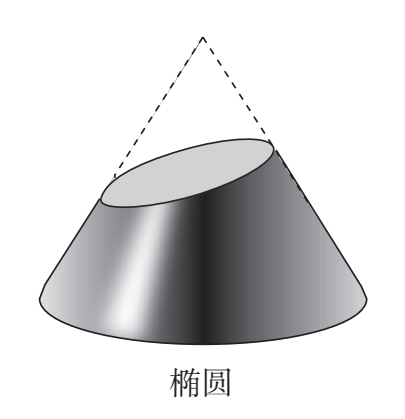如果它截切的角度与锥体的斜率相同，就会得到一条抛物线（图2–8）。
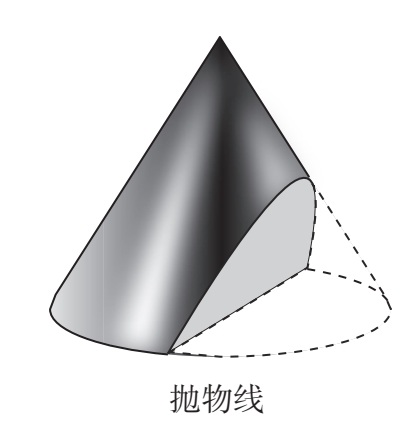求解抛物线弓形的面积
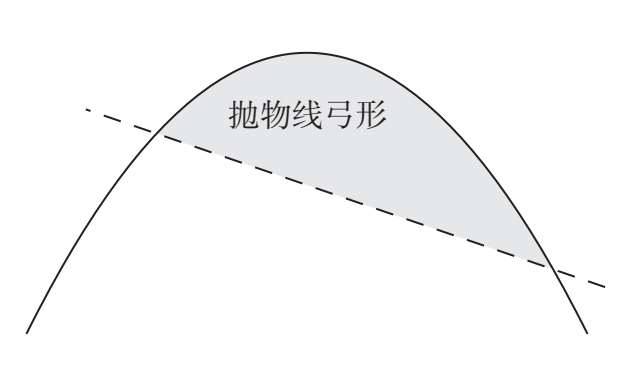
切点，它确定了大三角形的第三个角的位置，另外两个角的顶点就是斜线与抛物线的交 点。
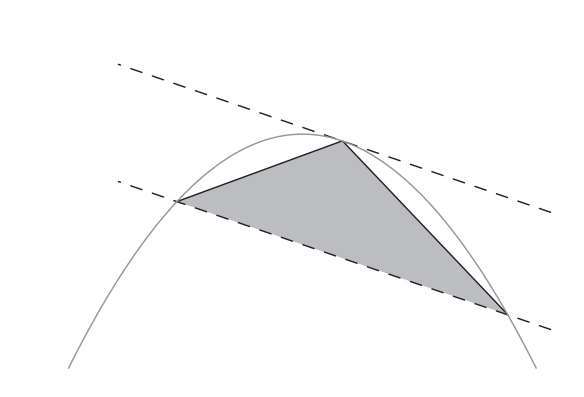某一层级三角形的总面积总是其上一层级三角形总面积的1/4。
这是一个无穷级数，其中每一项都是它前一项的1/4。
抛物线弓形的面积是大三角形面积的4/3。
奶酪论证
双重归谬法或双重反证法
阿基米德方法
从计算机动画到面部手术
探索运动之谜
3. 运动定律的探索之旅
亚里士多德的世界观
以火星为例，人们观测到它在接近两年的公转周期里，有大约11周的时间在逆行。今天， 我们可以用摄影的方式来捕捉它的逆行轨迹。2005年，天体摄影师唐克·特泽尔拍摄了一 组火星快照，共35张，前后两张照片的拍摄时间均间隔一周左右。
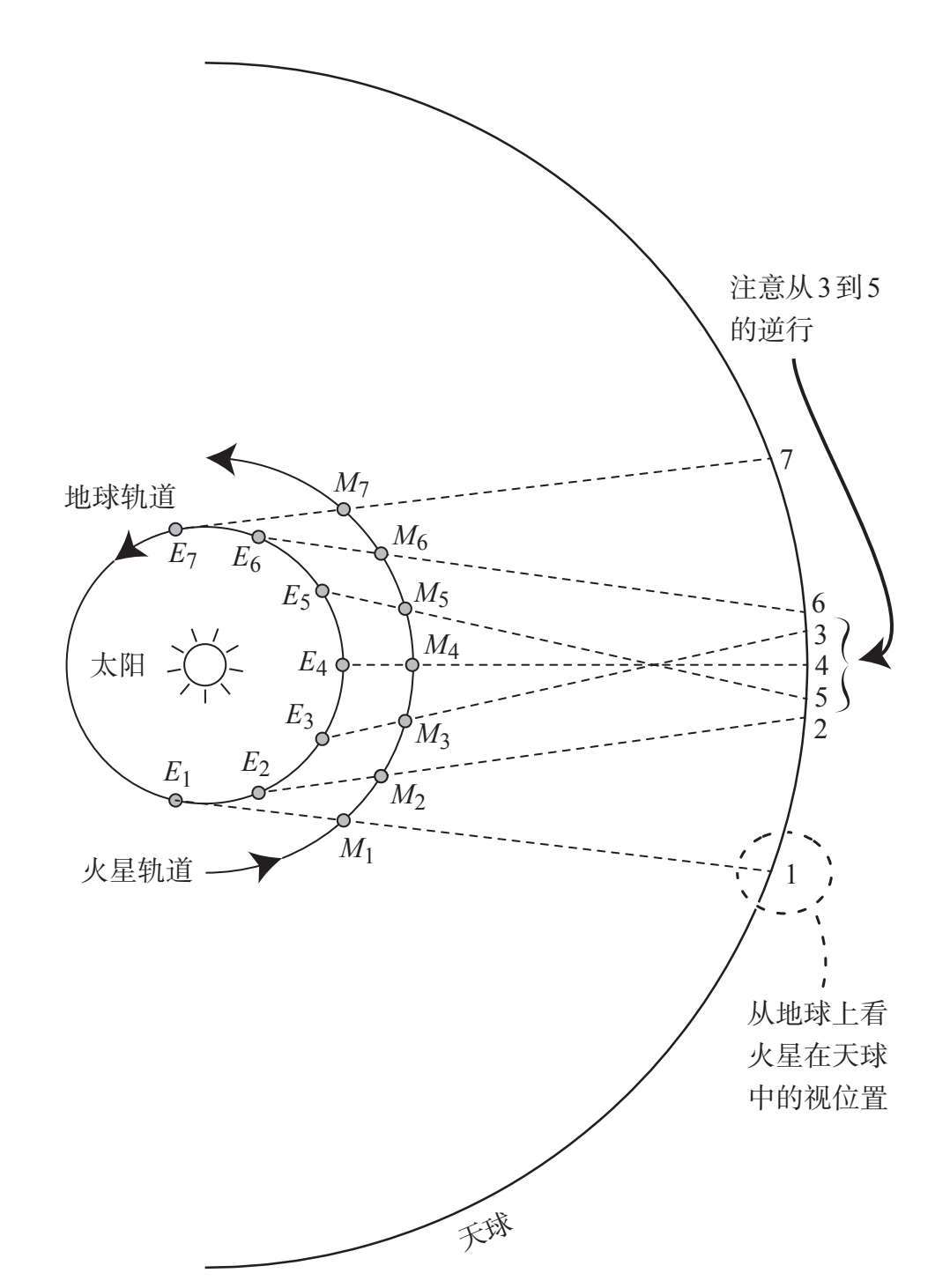经验表明，如果你看着远处的某个物体，然后换个地方再看一次，那么在一个更远背景
的衬托下，这个物体的位置看上去似乎有所改变，这种效应被称为视差。
伽利略出场
下落、滚动与奇数定律
科学极简主义的艺术
从摆动的吊灯到GPS
1962年，22岁的剑桥大学研究生布赖恩·约瑟夫森做出了这样一个预测：在接近绝对零度 的温度条件下，成对的超导电子可以来回隧穿一道难以穿透的绝缘屏障。 计数铯原子在其两种能态间来回转换时的振动次数，这种能态转换每秒钟要进行9 192 631 770次 GPS还让无线电话和数据网络保持同步，使它们能更高效地共享电磁波谱中的频率。
开普勒与行星运动之谜
开普勒第一定律：椭圆轨道
开普勒的第一个伟大发现是，所有行星都在椭圆轨道上运行
开普勒第二定律：相等的时间，相等的面积
如果我们在火星轨道上任意取两个时间间隔相等的点，不管它们在轨道的什么位置上， 矢径扫过的扇形面积总是相等（图3–9）。
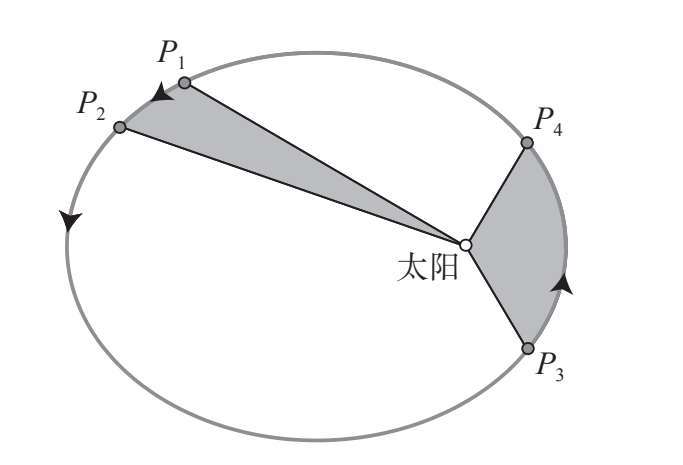第二定律说明，行星并不以恒定的速度运行。相反，离太阳越近，它们的运行速度就越
快。
开普勒第三定律：行星的公转周期
第三定律的要点很简单：一颗行星距离太阳越远，它的运行速度就越慢，公转一周所需 的时间也越长 开普勒第三定律就可以简化为 T2=a3
开普勒与伽利略的异同点
阴云密布
4. 微分学的黎明
代数在东方的崛起
代数的兴起与几何学的衰落
代数与几何学的邂逅
方程与曲线
在一起，会更好
费马vs笛卡儿
René Descartes 是有史以来最雄心勃勃的思想家之一。他在学术上无所畏惧、蔑视权威， 自我的程度之强不亚于他过人的天赋
笛卡儿致力于在理性、科学和怀疑主义的基础上重建人类知识
在他最有名的著作《方法论》中，尽管笛卡儿介绍了一种令人振奋的思考哲学问题的新方式 解析几何
寻找失传已久的发现方法——分析
这里所说的分析，指的是发现结果而不是证明结果的方法
行李箱的优化问题
费马微分学定理的雏形产生于他运用代数分析法解决优化问题的过程中，优化问题研 究的是如何以最佳方式做事情。根据具体情境，最佳可能意味着最快、最便宜、最大、 最有利可图和最有效等。
费马如何帮助了美国联邦调查局？
由于圆与周期密切相关，所以不管是季节循环、音叉振动，还是荧光灯和电力线发出的 60个周期/秒的嗡嗡声，只要循环现象发生，正弦波就会出现。那烦人的嗡嗡声恰恰是正 弦波每秒上下起伏60次发出的声音，这表明电网中的发电机也在以相同的频率旋转，并 产生交流电。哪里有圆周运动，哪里就有正弦波。
所有正弦波都可以用4个重要的统计数据来定义：周期、平均数、振幅和相位。 周期T表示正弦波完成一个周期所需的时间 正弦波的平均数是它的基线值b 波的振幅a可以告诉我们，一年中最长的昼长会比平均数多出多少分钟 波的相位c可以告诉我们，波在春分前后会向上穿过平均数。
所有这一切引出了一个极其重要的一般性观点：模式是让数据压缩成为可能的首要条件。 只有模式化的数据才能被压缩，而随机数据则不行
子波 子波比正弦波更加局部化，它们并不是在两个方向上周期性地无限延伸，而是 在时间或空间上急剧集中。
最短时间原理
他猜测光总是沿任意两点之间阻力最小的路径传播，换言之，光会沿着最快的路线行进
他由此证明了光会以最有效的方式传播——不是以最直接的方式，而是以最快的方式。在 光可以采取的所有可能的传播路径中，它知道（或者表现得好像它知道一样）如何尽可 能快地从这里到达那里。这是表明微积分以某种方式深植于宇宙操作系统的一个重要的 早期线索。
关于切线的争论
近在眼前的应许之地
5. 微积分的十字路口
微积分不再满足于静态的几何世界，而是痴迷于动态变化。它想解决的问题是：运动和变 化的规则是什么？我们能对未来做出哪些确定性预测呢？
一元函数微积分
函数的作用
事物的变化方式有三种：上升、下降或上下起伏。换句话说，就是成长、衰退或波动
幂函数
线性函数 Linear Function 其因变量y与自变量x成正比 对二次增长来说，改变量本身会随着x的增长而增大，这表明越往后函数值的增长越快。 二次增长
指数函数
幂函数 Power Function 诸如2x或10x之类的指数函数则描述了一种爆炸式增长，犹如雪球一般越滚越大 指数函数 Exponential Function 像2x和(1.01)x这样的指数函数中，数字2和1.01被称为函数的底数
10 的次方
对数
log(a×b)=log a+log b 反函数
自然对数及其指数函数
以它为底的指数函数的增长速率恰好等于这个函数本身。 ex的增长率就是ex本身。 极限 当n趋于无穷时，你的存款金额将趋于100与(1+1/n)n的乘积的极限，这个极限被定义为 数字e。尽管我们并不清楚该极限值是多少，但事实证明它大约为2.718 28…。
定义e，结果证明它是一个复杂的极限。无穷是e的固有属性，就像数字π是圆的固有属性一样
指数增长与指数式衰减的机制
微积分术语可表述为，ex是它自身的导数 Derivative 核链式反应也受到指数增长的支配。当一个铀原子分裂时，它会释放出中子，这些中子 可能会撞击其他原子并导致它们分裂，从而释放出更多中子，以此类推。如果不加以控 制，中子数量的指数增长就会引发核爆炸。
除了增长过程之外，衰减过程也可以用指数函数来描述 指数式衰减是指某个事物以与当前水平成正比的速度减少或者消耗
6. 变化率和导数
微积分的三大核心问题
微积分有三大核心问题：
斜率衡量的是变化率，而面积衡量的是变化的累积量
线性函数及其恒定的变化率
非线性函数及其不断变化的变化率
在放大无穷倍的极限情况下（相当于放大了我们感兴趣的那一点周围的一段无穷小的曲 线），被放大的那一段曲线应该接近于一条直线。如果是这样，这条极限直线就会被定 义为曲线上那一点的切线，它的斜率也会被定义为那一点的导数。
作为昼长变化率的导数
如果一个变量遵循完美的正弦波模式，那么它的变化率也是一个完美的正弦波，并且在 时间上提前了1/4个周期
正弦波 正弦波的变化率还是正弦波 由于圆的几何结构，任何正弦波及其导数（变化率）的波之间总有1/4个周期的位移 自我再生性质 假设有一群鲨鱼在捕食一群鱼，当这群鱼处于种群数量的最大值时，鲨鱼数量的增长速 率最快，因为有很多鱼可以吃。鲨鱼数量会继续增加，并在1/4个周期后达到最大值，而 此时鱼的数量已经开始下降，因为在1/4个周期之前，它们遭到了大肆捕食
作为瞬时速度的导数
瞬时速度 在任何时刻，博尔特都恰好身处某个地方，就像在快照里一样纹丝不动。既然如此，讨 论他在一瞬间的速度又有什么意义呢？速度只能出现在一个时间间隔内，而非一个瞬间。 将瞬时速度定义为一个极限，具体来说，就是在越来越短的时间间隔内平均速度的极限。 瞬间速度也是一个导数
插值法 但对数据分析师来说，它们既讨厌又烦人。我们真正想看到的是趋势，而不是波动
7. 隐秘的源泉
面积、积分和基本定理
运动使基本定理更直观
不管物体的运动有多么不规律，它的速度曲线下方累积到时间t的面积总会等于它在t小 时后行驶的距离
恒定的加速度
汽车每个时刻的速度都由线性函数v(t)=10t给出，其中数字10表示汽车的加速度。如果 加速度是其他常数，比如a，那么这个公式可以泛化为： v(t)=at
用油漆滚筒证明基本定理
比切线更重要的是它们的斜率，因为正是斜率引出了导数的概念 导数表明了斜率与速度之间的联系，更广泛地讲，是几何学和运动之间的联系
基本定理的意义
积分学的圣杯
面积问题旨在预测以不断变化的速率变化的事物与它随时间的累积程度之间的关系
它与银行账户的波动性流入和累计余额有关；它与世界人口的增长率和地球上的净人口 数有关；它与化疗药物在患者血液中不断变化的浓度和随时间的累积暴露剂量有关，因 为总暴露量会影响化疗药物的效果和毒性。面积问题之所以重要，是因为未来对我们而 言至关重要。
局部vs整体
一个孤寂的男孩
玩转幂级数
混搭大师
私密的微积分
8. 思维的虚构产物
眨眼之间
无穷小量
2.001 的立方
2的立方（2×2×2）是多少？答案当然是8。那么，2.001×2.001×2.001是多少？其结果肯 定略大于8，但到底大多少呢？ 2.001^3=8.012 006 001 其中：0.012 006 001=0.012+0.000 006+0.000 000 001 当我们问 2.001^3 是多少时，我们实际上问的是 (x+Δx)^3 等于多少 \((x+\delta x)^3 = x^3 + 3x^2\delta x + 3x (\delta x)^2 + (\delta x)^3\)
微分
我们可以把它缩减得更简单： (2+dx)^3 = 8+12dx (2+Δx)^3 展开为 8 + 12Δx + 6(Δx)^2 + (Δx)^3 6(dx)^2 + (dx)^3…舍弃了它们。作为超小和超超小的无穷小量，它们与 12dx 相比是完全 微不足道的 要保留 12dx…如果我们把它也舍弃了，就无法考虑任何变化量了
微分求导法
曲线的斜率是y的导数，即当Δx趋于0时Δy/Δx的极限。但从微分的角度看，斜率又是什么 呢？答案很简单：dy/dx
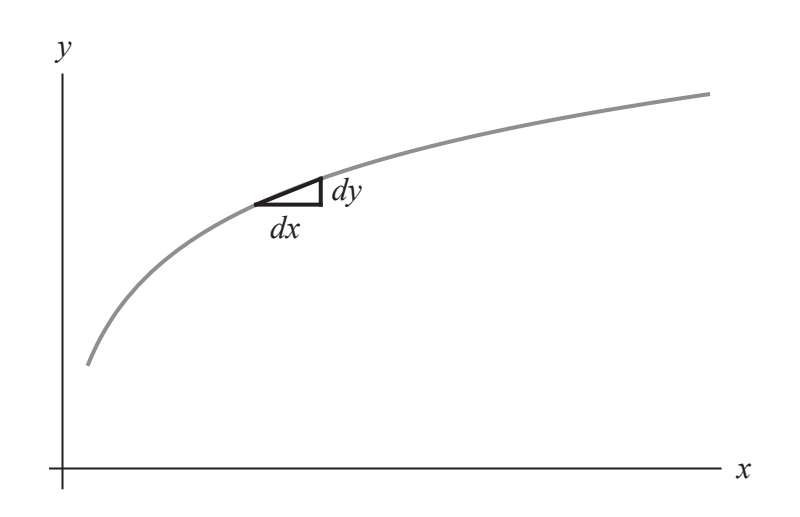无穷小量唯一的缺陷在于，它们并不存在，至少在实数系中如此
通过微分推导出基本定理
曲线下方的面积被视为无穷多个无穷小的矩形条的面积之和时，我们就可以把它写成：
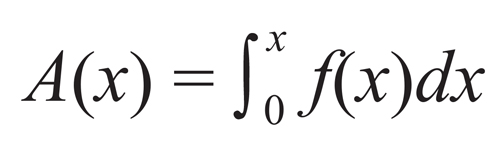
莱布尼茨是如何发现微分和基本定理的？
在微积分的帮助下对抗HIV
免疫系统每天清除的病毒颗粒数量为10亿个
9. 宇宙的逻辑
在很大程度上，生命的进化是一个在前体的基础上朝着更高级和更复杂的方向前进的故事， 微积分也是这样
在人类努力探索的每个领域，微分方程已经成为描述我们周围和内部事物（从亚原子域到 宇宙最远端）如何变化的通用框架了。
自然的逻辑
运动微分方程： F = ma 它描述的是，作用于一个运动物体的力 F 等于该物体的质量 m 与它的加速度 a 的乘积 发现引力的人不是牛顿，人们早已知道重物会下落。但没人知道引力的作用范围有多大， 它的尽头是天空吗？牛顿预感到引力可能会延伸到月球或更远的地方 自然拥有数学内核，自然现象可以从引力和运动定律等经验性公理通过逻辑推导得出”， 牛顿的这些想法让他们目瞪口呆
二体问题
牛顿力学与《隐藏人物》
牛顿微积分与《独立宣言》
连续体与离散集
随着物体数量的增加，一直到无穷多个粒子，微分方程又变得易于求解了……只要这些粒 子形成连续介质，而不是离散集
常微分方程与偏微分方程
常微分方程 这类微分方程只取决于一个自变量。 常微分方程描述的是，某个因素的无穷小的变化（比如无穷小的时间增量）如何引起其 他因素（比如行星的位置和病毒颗粒的浓度）的无穷小的变化。这样的方程之所以被称 为“常”微分方程，是因为它们只有一个自变量。
只要有且仅有一个自变量，这个微分方程就可以被视为常微分方程 常微分方程完全适用于包含一个或更多物体的离散系统，它们可以描述一艘宇宙飞船重 返大气层的运动
没有人会考虑用常微分方程为一碗汤的冷却过程建模。这不仅是因为有太多的粒子需要 处理，还因为它们的运动过于不规则、随意和不可知。
偏微分方程 之所以这样命名，是因为它们的每个自变量在引发变化的过程中都发挥 着各自的作用。
它们描述了连续系统的运动同时随空间和时间发生的变化，或者连续系统在两个或更多 维度的空间中运动的变化情况
偏微分方程与波音 787 客机
无处不在的偏微分方程
10. 波、微波炉和脑成像
1807年，傅里叶 出了一个偏微分方程，可用于预测物体（比如一根炽热的铁棒）在冷却过程中温度的变化情况 它包含两个自变量的导数：一个是时间（t）的无穷小变化量，另一个是铁棒上位置（x） 的无穷小变化量。
弦理论
为什么是正弦波？
正弦波的优点在于，它们可以与导数“相处得十分融洽”。具体来说，一个正弦波的导数 是另一个正弦波，两者之间存在1/4个周期的位移
为什么有人要对某个东西求导两次呢？因为自然一直是这样做的，更确切地说，我们的 自然模型一直是这样做的。比如，在牛顿的运动定律F=ma中，加速度a就涉及两次求导。 想知道其中的原因，你需要记住加速度是速度的导数，而速度又是距离的导数。
加速度是距离的二阶导数
二阶导数 驻波不会沿着弦或铁棒移动，而会待在原地；尽管它们会上下振动，但从不传播。更引 人注目的是，驻波会以单一频率振动，这在波的世界里非常少见
振动模态的可视化：克拉德尼图形
最值得尊崇的勇气
微波炉
为什么微波炉最初被称作雷达灶？
CT与脑成像
我们生活在一个三维世界里，为什么还会有人想要研究四维大脑呢？科马克解释说： 这些成果有什么用呢？答案是：我不知道。它们几乎肯定会在偏微分方程理论中产生一 些定理，而且有的定理可能会在MRI或超声成像中得到应用。但这尚不确定，也无关紧要。 昆图和我正在研究这些课题，因为它们本身就是有趣的数学问题，这才是科学的真谛。
11. 微积分的未来
微积分可以由它的信条来定义：在解决关于任意连续体的难题时，先把它切分成无穷多个 部分，然后一一求解，最后通过把各个部分的答案组合起来去解决原始的难题。我把这个 信条称作无穷原则。 微积分是用于研究任何事物——任何模式，任何曲线，任何运动，任何自然过程、系统或现 象——的想法与方法的庞杂集合，这些事物的变化平稳而连续，符合无穷原则。
DNA的缠绕数
20世纪70年代初，美国数学家布洛克·富勒 他发明了一个叫作DNA缠绕数[2]的量，用积分和导数推导出它的公式，证明了关于它的 某些定理，从而明确了针对螺旋和缠绕的守恒定律
决定论及其局限性
非线性动力学 非线性、混沌和复杂系统 拉普拉斯设想了一个全知全能的智慧生物——拉普拉斯妖，它可以追踪宇宙中所有原子的 所有位置，还有作用于它们的所有力。“如果这个智慧生物也能对这些数据进行分析，” 他写道，“那就没有什么是不确定的了，[2]未来也会像过去一样呈现在它眼前。”
19世纪早期，法国数学家和天文学家皮埃尔–西蒙·拉普拉斯 陀螺就是一种刚体，它非常坚固，由无穷多个点组成，所以陀螺是比牛顿研究的单点状 粒子更复杂的机械对象。在天文学和空间科学中，刚体的运动对于描述从土卫七（土星 的一个土豆状的小卫星）的混沌翻滚[4]到太空舱或卫星的规律旋转等现象都具有重要意 义。
刚体动力学 刚体是针对不能弯曲或变形的物体的一种数学抽象，它的所有点都刚性地连接在一起 柯瓦列夫斯卡娅得出了两个重要结果。一个重要的结果是，她全面分析和解决了陀螺的运动问题 另一个重要的结果是，她证明了不可能存在其他可解陀螺。她发现的正是最后一个，而 余下的陀螺都是不可解的，这意味着它们的动力学问题也不可能用牛顿式公式来解决
她限定了微积分的适用范围。一个陀螺即可挑战拉普拉斯妖，从原则上说，找到关于宇 宙命运的公式也无望了。
非线性
线性系统 线性系统中，整体等于部分之和，这是线性的第一个关键特性。线性的第二个特性是，原因与结果成正比 大部分日常活动显然都是非线性的，如果同时听你最喜欢的两首歌，你不会得到双倍的快乐 线性的一大优势在于，它为还原论思维的运用创造了条件 如果一个系统是非线性的，它的行为就不可能用公式来预测，即使该行为是完全确定的。 换句话说，决定论并不意味着可预测性
混沌
三体问题 二体问题 混沌 Chaos theory 混沌系统不是随机的，而是确定的，因此短期来看它们是可预测的。但长期来看，它们 对微小的扰动十分敏感，以至于在许多方面实际上都是随机的。 混沌系统在某个时间之前是完全可以预测的，这个时间被称为可预测性时界